백준🔗
1182번: 부분수열의 합
첫째 줄에 정수의 개수를 나타내는 N과 정수 S가 주어진다. (1 ≤ N ≤ 20, |S| ≤ 1,000,000) 둘째 줄에 N개의 정수가 빈 칸을 사이에 두고 주어진다. 주어지는 정수의 절댓값은 100,000을 넘지 않는다.
www.acmicpc.net
문제

간단 풀이
"1208_부분수열의 합 2" 문제를 풀려다가 감이 잘 잡히지 않아서 이 문제부터 먼저 풀어 보았다.
수열의 원소 개수인 N이 최대 20이기 때문에 부분 수열은 최대 2^20개가 있을 수 있다.
2^20 = (2^10)*(2^10) => 대략 100만 정도.. (정확한 계산값은 2^20 = 1,048,576)
하나의 부분 순열에 대해 원소의 합을 구하는 데는 최대 N만큼이 든다고 하면 최대 O(N*2^N) 정도의 시간복잡도가 소요된다고 계산이 된다. 모든 부분수열을 구해서 원소의 합을 구하는 완전탐색을 해도 충분히 시간 내에 해결이 가능하겠다는 판단이 들었고, 아래의 코드대로 구현을 했다
보통 부분 수열을 구할 때 재귀를 많이 사용한다.
원소를 하나씩 보면서 1) 해당 원소를 포함하는 경우 2) 해당 원소를 포함하지 않는 경우에 대해 다시 재귀함수를 부르는 방식으로 나아가면 원소를 끝까지 탐색했을 때 모든 경우의 부분수열을 구할 수 있다.
그러나 나는 이번에 비트마스킹을 사용했다.
싸피 1학기 수업에서 배웠던 방법인데, 재귀함수를 돌릴 필요가 없어서 원리만 이해한다면 더 간단한 방식이라고 생각이 된다. 한동안 잘 안 썼던 방법이라 연습도 해볼 겸 비트마스킹으로 구현했다.
2중 for문 중 첫 번째 for문은 2^N개의 부분집합들을 하나씩 보는 것이다.
두 번째 for문은 각각의 부분집합에 원소가 포함되는지 여부를 따져서 포함되는 경우 내가 원하는 로직을 실행해주면 된다.
예를 들어.. 원소의 개수가 2개인 수열을 생각해보자.
1) i = 0
1-1) 부분집합 0에 0번째 원소가 포함되어 있는지 판단 => 포함 x
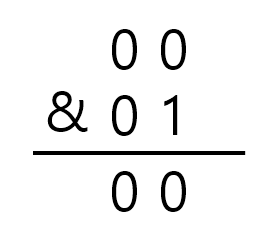
1-2) 부분집합 0에 1번째 원소가 포함되어 있는지 판단 => 포함 x
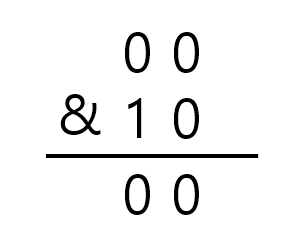
2) i = 1
2-1) 부분집합 1에 0번째 원소가 포함되어 있는지 판단 => 포함 o

2-2) 부분집합 1에 1번째 원소가 포함되어 있는지 판단 => 포함 x

3) i = 2
3-1) 부분집합 2에 0번째 원소가 포함되어 있는지 판단 => 포함 x
3-2) 부분집합 2에 1번째 원소가 포함되어 있는지 판단 => 포함 o
4) i = 3
4-1) 부분집합 3에 0번째 원소가 포함되어 있는지 판단 => 포함 o
4-2) 부분집합 3에 1번째 원소가 포함되어 있는지 판단 => 포함 o
위와 같은 원리로 각각의 부분집합에 어떤 원소들이 포함되어 있는지를 파악할 수 있다.
코드
import java.io.*;
import java.util.*;
public class Main {
public static void main(String[] args) throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
int N = Integer.parseInt(st.nextToken()); // 정수 개수
int S = Integer.parseInt(st.nextToken()); // 합이 S인 부분수열 개수 구하기
int[] arr = new int[N];
st = new StringTokenizer(br.readLine());
for (int i = 0; i < N; i++) {
arr[i] = Integer.parseInt(st.nextToken());
}
// 비트마스킹으로 부분순열 구하기
int cnt = 0;
for (int i = 1; i < (1 << N); i++) { // 부분집합 i (크기가 양수이니까 0 제외)
int sum = 0; // 부분집합 i에 포함되는 원소들의 합
for (int j = 0; j < N; j++) { // j번째 원소
// 부분집합 i에 j번째 원소가 포함되는 경우
if ((i & (1 << j)) > 0) {
sum += arr[j];
}
}
if (sum == S)
cnt++;
}
System.out.println(cnt);
}
}
참고 자료
백준🔗
1182번: 부분수열의 합
첫째 줄에 정수의 개수를 나타내는 N과 정수 S가 주어진다. (1 ≤ N ≤ 20, |S| ≤ 1,000,000) 둘째 줄에 N개의 정수가 빈 칸을 사이에 두고 주어진다. 주어지는 정수의 절댓값은 100,000을 넘지 않는다.
www.acmicpc.net
문제

간단 풀이
"1208_부분수열의 합 2" 문제를 풀려다가 감이 잘 잡히지 않아서 이 문제부터 먼저 풀어 보았다.
수열의 원소 개수인 N이 최대 20이기 때문에 부분 수열은 최대 2^20개가 있을 수 있다.
2^20 = (2^10)*(2^10) => 대략 100만 정도.. (정확한 계산값은 2^20 = 1,048,576)
하나의 부분 순열에 대해 원소의 합을 구하는 데는 최대 N만큼이 든다고 하면 최대 O(N*2^N) 정도의 시간복잡도가 소요된다고 계산이 된다. 모든 부분수열을 구해서 원소의 합을 구하는 완전탐색을 해도 충분히 시간 내에 해결이 가능하겠다는 판단이 들었고, 아래의 코드대로 구현을 했다
보통 부분 수열을 구할 때 재귀를 많이 사용한다.
원소를 하나씩 보면서 1) 해당 원소를 포함하는 경우 2) 해당 원소를 포함하지 않는 경우에 대해 다시 재귀함수를 부르는 방식으로 나아가면 원소를 끝까지 탐색했을 때 모든 경우의 부분수열을 구할 수 있다.
그러나 나는 이번에 비트마스킹을 사용했다.
싸피 1학기 수업에서 배웠던 방법인데, 재귀함수를 돌릴 필요가 없어서 원리만 이해한다면 더 간단한 방식이라고 생각이 된다. 한동안 잘 안 썼던 방법이라 연습도 해볼 겸 비트마스킹으로 구현했다.
2중 for문 중 첫 번째 for문은 2^N개의 부분집합들을 하나씩 보는 것이다.
두 번째 for문은 각각의 부분집합에 원소가 포함되는지 여부를 따져서 포함되는 경우 내가 원하는 로직을 실행해주면 된다.
예를 들어.. 원소의 개수가 2개인 수열을 생각해보자.
1) i = 0
1-1) 부분집합 0에 0번째 원소가 포함되어 있는지 판단 => 포함 x
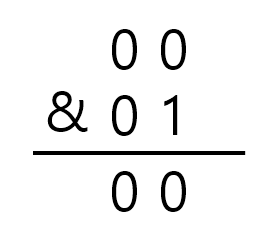
1-2) 부분집합 0에 1번째 원소가 포함되어 있는지 판단 => 포함 x
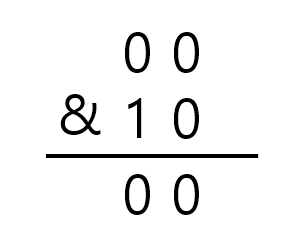
2) i = 1
2-1) 부분집합 1에 0번째 원소가 포함되어 있는지 판단 => 포함 o

2-2) 부분집합 1에 1번째 원소가 포함되어 있는지 판단 => 포함 x

3) i = 2
3-1) 부분집합 2에 0번째 원소가 포함되어 있는지 판단 => 포함 x
3-2) 부분집합 2에 1번째 원소가 포함되어 있는지 판단 => 포함 o
4) i = 3
4-1) 부분집합 3에 0번째 원소가 포함되어 있는지 판단 => 포함 o
4-2) 부분집합 3에 1번째 원소가 포함되어 있는지 판단 => 포함 o
위와 같은 원리로 각각의 부분집합에 어떤 원소들이 포함되어 있는지를 파악할 수 있다.
코드
import java.io.*;
import java.util.*;
public class Main {
public static void main(String[] args) throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
int N = Integer.parseInt(st.nextToken()); // 정수 개수
int S = Integer.parseInt(st.nextToken()); // 합이 S인 부분수열 개수 구하기
int[] arr = new int[N];
st = new StringTokenizer(br.readLine());
for (int i = 0; i < N; i++) {
arr[i] = Integer.parseInt(st.nextToken());
}
// 비트마스킹으로 부분순열 구하기
int cnt = 0;
for (int i = 1; i < (1 << N); i++) { // 부분집합 i (크기가 양수이니까 0 제외)
int sum = 0; // 부분집합 i에 포함되는 원소들의 합
for (int j = 0; j < N; j++) { // j번째 원소
// 부분집합 i에 j번째 원소가 포함되는 경우
if ((i & (1 << j)) > 0) {
sum += arr[j];
}
}
if (sum == S)
cnt++;
}
System.out.println(cnt);
}
}
