백준🔗
11049번: 행렬 곱셈 순서
첫째 줄에 입력으로 주어진 행렬을 곱하는데 필요한 곱셈 연산의 최솟값을 출력한다. 정답은 231-1 보다 작거나 같은 자연수이다. 또한, 최악의 순서로 연산해도 연산 횟수가 231-1보다 작거나 같
www.acmicpc.net
문제
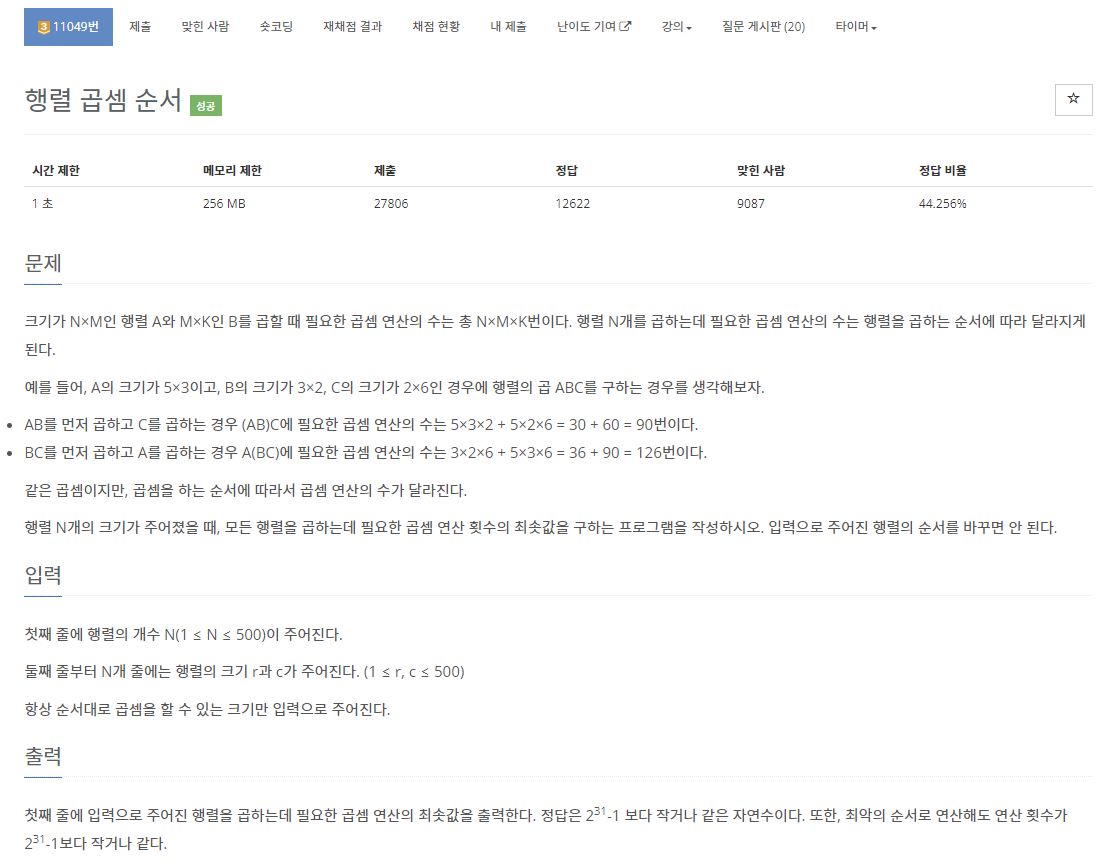
간단 풀이
구현하고 나니 코드 길이는 짧은데 풀이 과정은 쉽지 않았다..
행렬은 입력으로 주어진 순서를 바꾸면 안되기 때문에 주어진 순서에서 어떤 행렬끼리 먼저 계산할 것인지 선택만 할 수 있다. 그러나 어떤 방식으로 선택해 나가야 할 것인지, 중간중간 계산값은 어떻게 저장해야 할 지 감이 잘 오지 않았다.
어찌됐든 행렬 곱셈을 반복적으로 수행하기 때문에 dp배열을 사용해보자 생각을 했다.
처음에는 1차원 배열을 생각해서
dp[i] : i번째 행렬까지 있을 때의 곱셈 연산 최솟값
이라고 dp 배열을 정의해 봤다. 그러나 i번째 행렬이 있을 때와 없을 때로 나눠서 계산을 하는 것이 의미가 없다는 사실을 깨달았다. i번째와 i-1번째 행렬을 제일 처음 계산해야 할 수도 있고, 가장 마지막 순서로 계산해야 할 수도 있는데 각각에 따라 계산 결과와 순서가 너무 달라지기 때문에 1차원 배열로는 충분함 정보를 담지 못했다.
여기서 막혀서 고민하다가 다른 코드들을 참고해서 해결할 수 있었다..!!
해결방법은 dp를 2차원으로 정의하는 것이었다.
dp[i][j] : i부터 j번째까지 행렬의 곱셈 연산 최솟값
위와 같이 정의하면 필요한 정보들을 담을 수 있었다. 1차원 배열로 생각했을 때는 마지막 행렬만 고려했기 때문에 정보가 충분하지 못했는데 2차원으로 확장하면서 처음 행렬에 대해서도 나타낼 수 있었던 것이다.
행렬 A, B, C, D가 있을 때
A부터 C까지의 행렬을 곱할 때 필요한 곱셈 연산 수는
1) A(BC)
2) (AB)C
2가지 중 최소값을 구하면 된다.
B부터 D까지의 행렬을 곱할 때 필요한 곱셈 연산 수는
1) B(CD)
2) (BC)D
2가지 중 최소값을 구하면 된다.
A부터 D까지의 행렬을 곱할 때 필요한 곱셈 연산 수는
1) A(BCD)
2) (AB)(CD)
3) (ABC)D
3가지 중 최소값을 구하면 된다.
그림으로 나타내는 것이 이해가 쉽겠지만... 그 부분은 밑에 첨부한 다른 블로그를 참고하면 좋다!!
어쨌든 위와 같이 부분 문제들을 반복해서 사용하는 형태로 나타나기 때문에 dp를 적용해서 풀이해주면 된다!!
코드
import java.io.*;
import java.util.*;
public class Main {
public static void main(String[] args) throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int N = Integer.parseInt(br.readLine()); // 행렬 개수
int[][] arr = new int[N][2];
for (int i = 0; i < N; i++) {
StringTokenizer st = new StringTokenizer(br.readLine());
arr[i][0] = Integer.parseInt(st.nextToken());
arr[i][1] = Integer.parseInt(st.nextToken());
}
// dp[i][j] : i부터 j번째까지 행렬의 곱셈 연산 최솟값
int[][] dp = new int[N][N];
for (int k = 1; k < N; k++) { // 계단식으로 들어가는 정도
for (int i = 0; i + k < N; i++) { // 행
dp[i][i + k] = Integer.MAX_VALUE;
for (int j = i; j < i + k; j++) { // 열 0~직전까지 비교해보기
dp[i][i + k] = Math.min(dp[i][i + k],
dp[i][j] + dp[j + 1][i + k] + arr[i][0] * arr[j][1] * arr[i + k][1]);
}
}
}
System.out.println(dp[0][N - 1]);
}
}
참고 자료
[DP] 백준 - 행렬 곱셈 순서 11049번
행렬 곱셈 순서 11049번 모든 행렬을 곱하는데 필요한 곱셈 연산 횟수의 최솟값을 구하는 프로그램을 작성하시오. 예시 : ABCD의 행렬의 최솟값을 구하기 위해서는 A(BCD) (AB)(CD) (ABC)D ABCD중 최솟값을
velog.io
[백준 11049번] 행렬 곱셈 순서 (python)
문제 크기가 N×M인 행렬 A와 M×K인 B를 곱할 때 필요한 곱셈 연산의 수는 총 N×M×K번이다. 행렬 N개를 곱하는데 필요한 곱셈 연산의 수는 행렬을 곱하는 순서에 따라 달라지게 된다. 예를 들어, A의
ddiyeon.tistory.com
백준🔗
11049번: 행렬 곱셈 순서
첫째 줄에 입력으로 주어진 행렬을 곱하는데 필요한 곱셈 연산의 최솟값을 출력한다. 정답은 231-1 보다 작거나 같은 자연수이다. 또한, 최악의 순서로 연산해도 연산 횟수가 231-1보다 작거나 같
www.acmicpc.net
문제

간단 풀이
구현하고 나니 코드 길이는 짧은데 풀이 과정은 쉽지 않았다..
행렬은 입력으로 주어진 순서를 바꾸면 안되기 때문에 주어진 순서에서 어떤 행렬끼리 먼저 계산할 것인지 선택만 할 수 있다. 그러나 어떤 방식으로 선택해 나가야 할 것인지, 중간중간 계산값은 어떻게 저장해야 할 지 감이 잘 오지 않았다.
어찌됐든 행렬 곱셈을 반복적으로 수행하기 때문에 dp배열을 사용해보자 생각을 했다.
처음에는 1차원 배열을 생각해서
dp[i] : i번째 행렬까지 있을 때의 곱셈 연산 최솟값
이라고 dp 배열을 정의해 봤다. 그러나 i번째 행렬이 있을 때와 없을 때로 나눠서 계산을 하는 것이 의미가 없다는 사실을 깨달았다. i번째와 i-1번째 행렬을 제일 처음 계산해야 할 수도 있고, 가장 마지막 순서로 계산해야 할 수도 있는데 각각에 따라 계산 결과와 순서가 너무 달라지기 때문에 1차원 배열로는 충분함 정보를 담지 못했다.
여기서 막혀서 고민하다가 다른 코드들을 참고해서 해결할 수 있었다..!!
해결방법은 dp를 2차원으로 정의하는 것이었다.
dp[i][j] : i부터 j번째까지 행렬의 곱셈 연산 최솟값
위와 같이 정의하면 필요한 정보들을 담을 수 있었다. 1차원 배열로 생각했을 때는 마지막 행렬만 고려했기 때문에 정보가 충분하지 못했는데 2차원으로 확장하면서 처음 행렬에 대해서도 나타낼 수 있었던 것이다.
행렬 A, B, C, D가 있을 때
A부터 C까지의 행렬을 곱할 때 필요한 곱셈 연산 수는
1) A(BC)
2) (AB)C
2가지 중 최소값을 구하면 된다.
B부터 D까지의 행렬을 곱할 때 필요한 곱셈 연산 수는
1) B(CD)
2) (BC)D
2가지 중 최소값을 구하면 된다.
A부터 D까지의 행렬을 곱할 때 필요한 곱셈 연산 수는
1) A(BCD)
2) (AB)(CD)
3) (ABC)D
3가지 중 최소값을 구하면 된다.
그림으로 나타내는 것이 이해가 쉽겠지만... 그 부분은 밑에 첨부한 다른 블로그를 참고하면 좋다!!
어쨌든 위와 같이 부분 문제들을 반복해서 사용하는 형태로 나타나기 때문에 dp를 적용해서 풀이해주면 된다!!
코드
import java.io.*;
import java.util.*;
public class Main {
public static void main(String[] args) throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int N = Integer.parseInt(br.readLine()); // 행렬 개수
int[][] arr = new int[N][2];
for (int i = 0; i < N; i++) {
StringTokenizer st = new StringTokenizer(br.readLine());
arr[i][0] = Integer.parseInt(st.nextToken());
arr[i][1] = Integer.parseInt(st.nextToken());
}
// dp[i][j] : i부터 j번째까지 행렬의 곱셈 연산 최솟값
int[][] dp = new int[N][N];
for (int k = 1; k < N; k++) { // 계단식으로 들어가는 정도
for (int i = 0; i + k < N; i++) { // 행
dp[i][i + k] = Integer.MAX_VALUE;
for (int j = i; j < i + k; j++) { // 열 0~직전까지 비교해보기
dp[i][i + k] = Math.min(dp[i][i + k],
dp[i][j] + dp[j + 1][i + k] + arr[i][0] * arr[j][1] * arr[i + k][1]);
}
}
}
System.out.println(dp[0][N - 1]);
}
}
참고 자료
[DP] 백준 - 행렬 곱셈 순서 11049번
행렬 곱셈 순서 11049번 모든 행렬을 곱하는데 필요한 곱셈 연산 횟수의 최솟값을 구하는 프로그램을 작성하시오. 예시 : ABCD의 행렬의 최솟값을 구하기 위해서는 A(BCD) (AB)(CD) (ABC)D ABCD중 최솟값을
velog.io
[백준 11049번] 행렬 곱셈 순서 (python)
문제 크기가 N×M인 행렬 A와 M×K인 B를 곱할 때 필요한 곱셈 연산의 수는 총 N×M×K번이다. 행렬 N개를 곱하는데 필요한 곱셈 연산의 수는 행렬을 곱하는 순서에 따라 달라지게 된다. 예를 들어, A의
ddiyeon.tistory.com
